
 |
Eager Space | Videos | All Video Text | Support | Community | About |
|---|



A while back Elon said the following...
(read)
That's a very interesting statement and I'm curious about whether it is correct.
To figure that out, we'll need to answer two questions:
The first is "how would increased gravity effect rockets?", and the second is whether that effect is bigger for reusable rockets.
To answer these questions - and to see if Elon is correct - we need to dig into the physics. This will get complicated for a minute or two and then it will get simpler. This part will not be on the test.
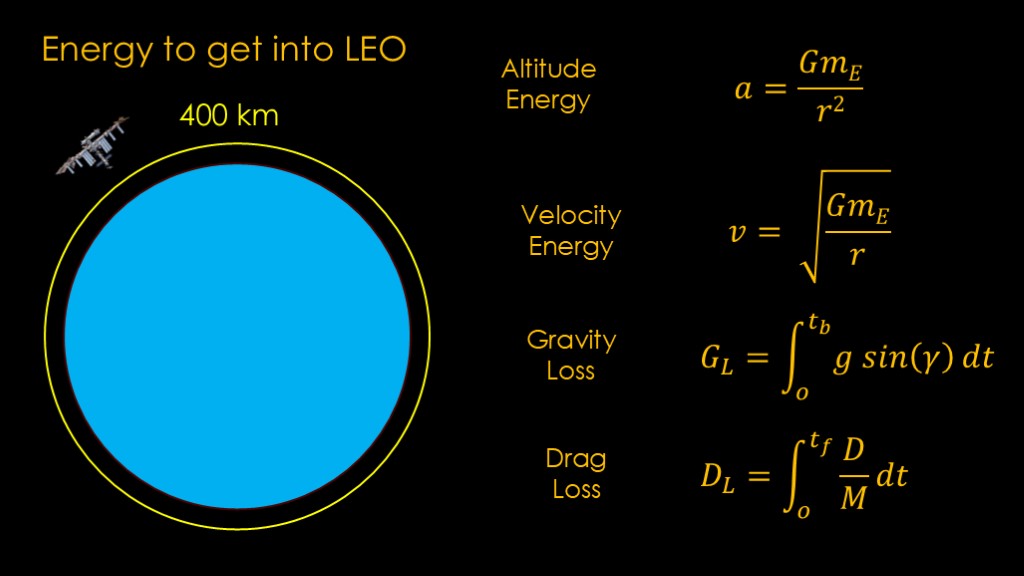
The energy required to get into a 400 kilometer orbit - about where the space station orbits - is determined by a number of factors.
We need to get up from the earth's surface to orbital altitude, and we can express that using this equation.
We then need to get up to orbital velocity, and we can figure out the energy cost using this equation.
Then we need to deal with the losses. We waste energy fighting gravity to get into orbit, and we waste energy fighting against drag, and there are two equations to estimate that.
We add all these up, and we get a very precise answer that is wrong. It's wrong because treating the altitude and velocity as separate quantities assumes that rockets are launched to the target altitude and then turn sideways. They don't do this because it's less efficient to do so.
The robust way to come up with the true energy cost is with a simulation that calculates all of these values on the fly. That's a lot of work and different rocket architectures fly different trajectories to minimize losses.
I'm not that ambitious, so I'm going to make what is often known as a simplifying assumption.
The drag loss is fairly small, so we will just ignore it.
All three of the remaining terms depend on gravity or the mass of the earth but the velocity energy is the largest one when , so I'm going to ignore the other two and just look at the velocity energy.
It won't give us the right answer, but it will give us an answer that is close enough.
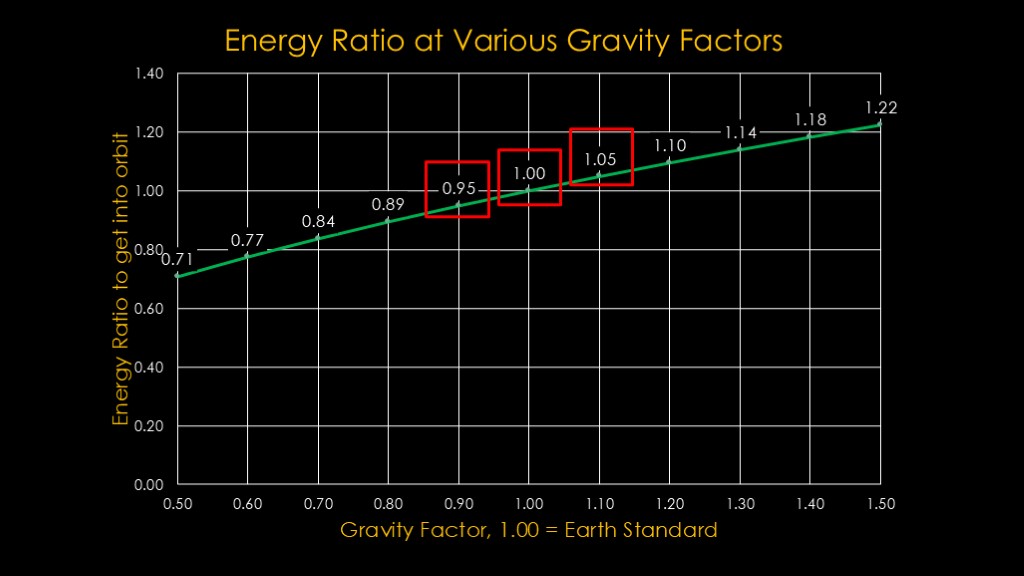
A little time with Excel yielded this graph, which summarizes the change in energy required to get into orbit in different gravity environments.
In the middle we see that at earth standard gravity the ratio is 1.0.
If we move out, a 10% reduction in earth gravity results in an energy ratio of 0.95 and a 10% increase results in a ratio of 1.05.
We now have some numbers that we can plug into a real example...

Which will of course be the Falcon 9, which I chose because it's very familiar, it has both expendable and partially reusable modes, I already have a model for it, and it's the cutest rocket around.
My model is written in Excel and is based on the rocket equation. I can feed in a payload amount and it will tell me how much delta v - how much energy - the Falcon 9 can give a payload of that mass. If you want to know more about the rocket equation, see my video "the care and feeding of the rocket equation".
We can plug in the maximum payload of the Falcon 9 to low earth orbit - 22,800 kilograms - and the model will say that the Falcon 9 can generate 9262 meters per second of delta v when flown in fully expendable mode.
That number is pretty much in the middle of the 9100-9400 meter per second range generally quoted to get into low earth orbit, so it's a validation that the model is decent.
I would also like to estimate the delta v required to fly in the other two modes. The maximum payload for a drone ship recovery is about 16,600 kilograms which yields a delta v of 10,090 meters per second, and the maximum payload for a return to launch site is about 13,000 kilograms and about 10,700 meters per second of delta v.
Those are the values that we see with standard earth gravity.
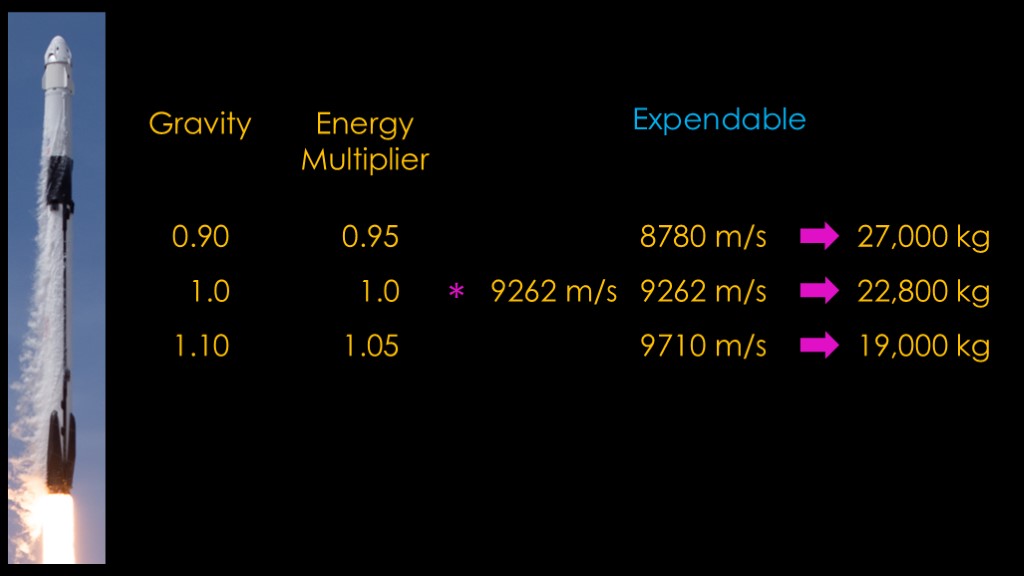
We can now combine the gravity data with the data from the model.
Our gravity data gave us these estimated energy multipliers. Multiplying our expendable delta V of 9262 meters per second by those multipliers, we get the required delta v for those three gravity scenarios. Not surprisingly, it takes less energy if gravity is lower and more energy if gravity is higher.
And then finally, we can use the Falcon 9 model to translate to the payload amounts Falcon 9 can carry while hitting those delta v values.
If gravity was 10% less, the Falcon 9 expendable payload would be about 27,000 kilograms, and if gravity was 10% greater, it would be about 19,000 kilograms.
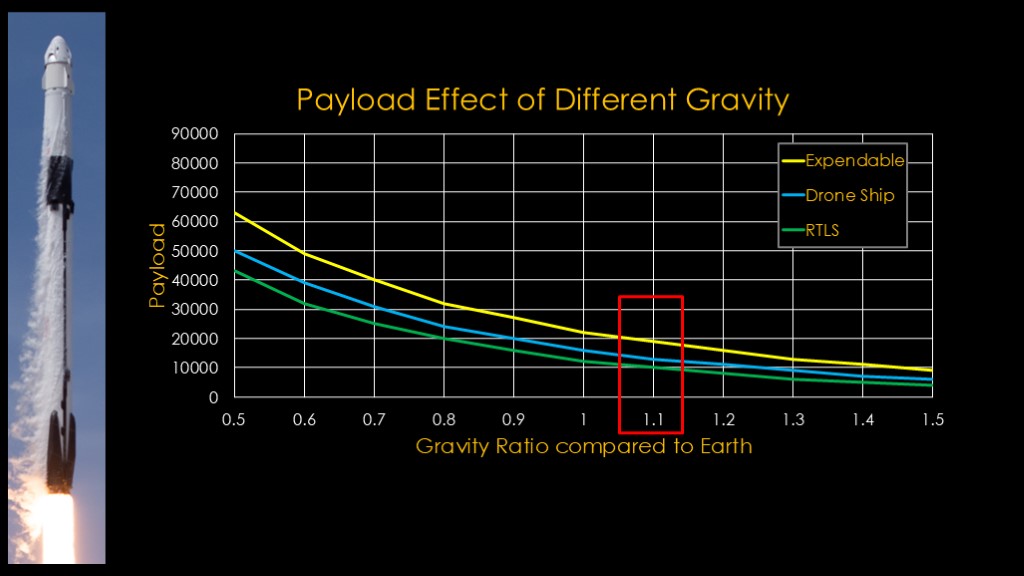
Do that for all three modes of the Falcon 9 and for a set of gravity ratios, and we get this chart.
There's definitely an effect, but it's not a huge one - 10% heavier gravity leads to 15-20% loss of payload. I would say that Falcon 9 isn't terribly sensitive to differences in gravity. Not close to the "impossible" situation that Elon talked about.
Let's look at that quote again...

He very specifically says full reusability, and since the Falcon 9 is only partially reusable, it isn't the scenario that he is talking about.
He's talking about Starship.
I took a similar approach with Starship and plugged its numbers into my model. Since it's very much under development, Starship is a moving - and sometimes exploding - target, so I used what I know about the OFT-4 flight and its supposed payload of about 50 tons.
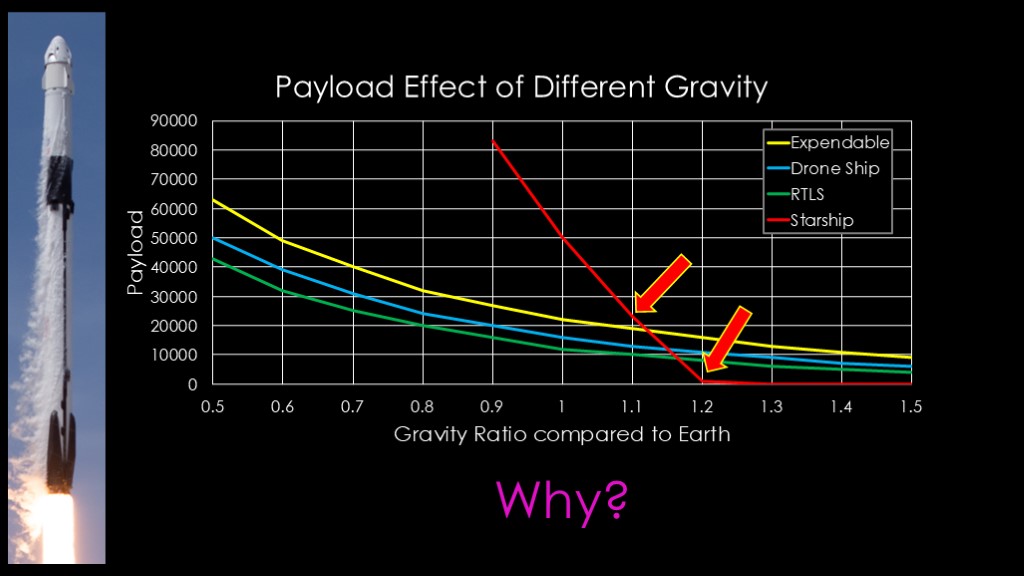
Add the starship data, and we get this graph.
Starship is hugely sensitive to changes in gravity, note that a 10% increase in gravity drops the payload from 50 tons down to 23 tons, and a 20% increase drops it all the way down to 1 ton.
At this point I hope you are asking "why, oh why is starship so bad?"
And for that we need to do a quick comparison between the second stages of falcon 9 and starship.
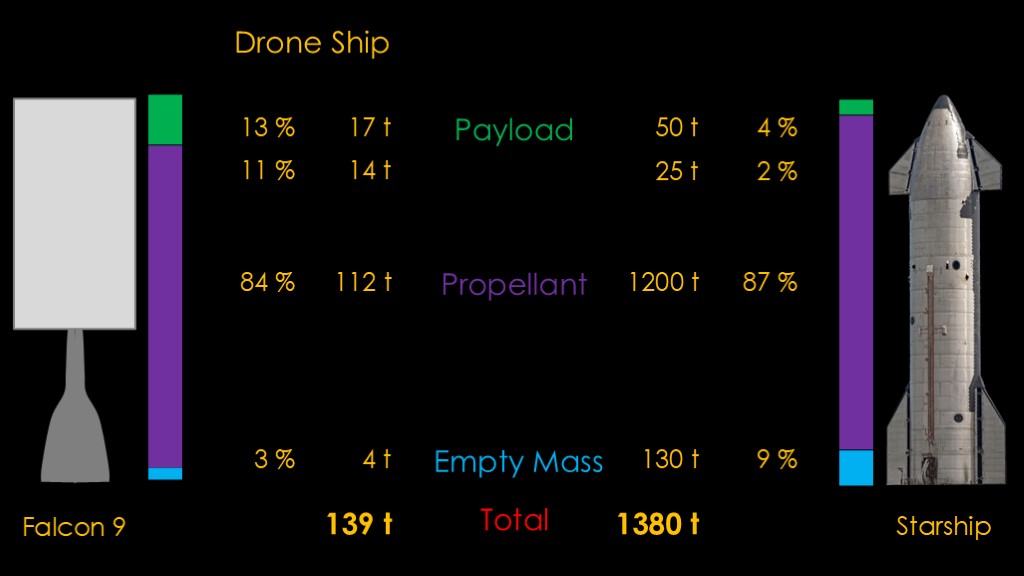
The Falcon 9 second stage is very light, with an empty mass of a little less than 4 tons. It carries 112 tons of propellant and, in droneship mode, 17 tons of payload. The total mass is 139 tons. We can look at this as percentages, with 3% going to empty mass, 84% to propellant, and 13% to payload.
Those are fairly typical numbers for a second stage.
Let's look at starship.
130 ton empty mass, 1200 tons propellant and 50 tons of payload , for a total of 1380 tons, or pretty close to 10 times the mass of the Falcon 9 second stage.
For percentages, the empty mass is 9% of the overall mass. That is the penalty of reuse; the stage requires coverage for the engines in the rear, heat shield tiles to survive reentry, and fins to guide it. It is also made of stainless steel, which is heavier than the aluminum lithium alloy used on the Falcon 9.
The propellant mass is a bit higher at 87%, and that leaves only 4 % for payload.
This explains why higher gravity is so much worse for starship; increased gravity reduces the mass a rocket can lift into orbit and the only place that reduction can come is in the payload. Higher gravity might require a 2% reduction in overall mass to compensate, and that only reduces the Falcon 9 payload from 17 tons to 14 tons, but 2% is half the payload for starship.

That's the story about starship and gravity, and I would consider the quote to be confirmed.
My model didn't quite show it was impossible at 10%, but I know that the SpaceX models are much better than mine is and we did see a very big effect.

If you enjoyed this video, please send me "Can't explain", a special edition DVD and book set.